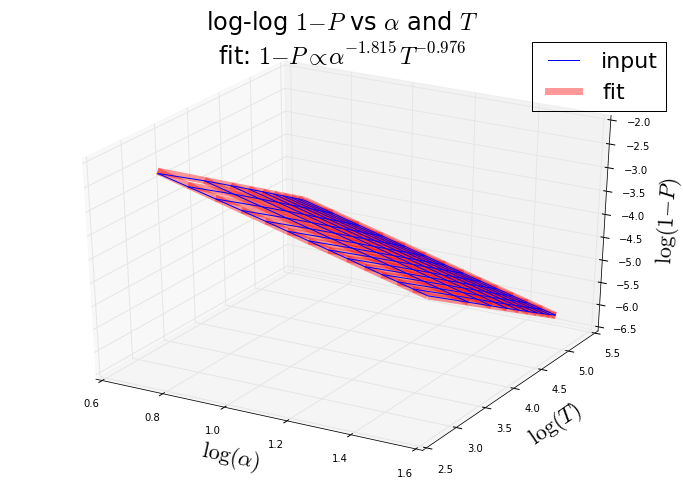
1−P∝α−1.8150T−0.976
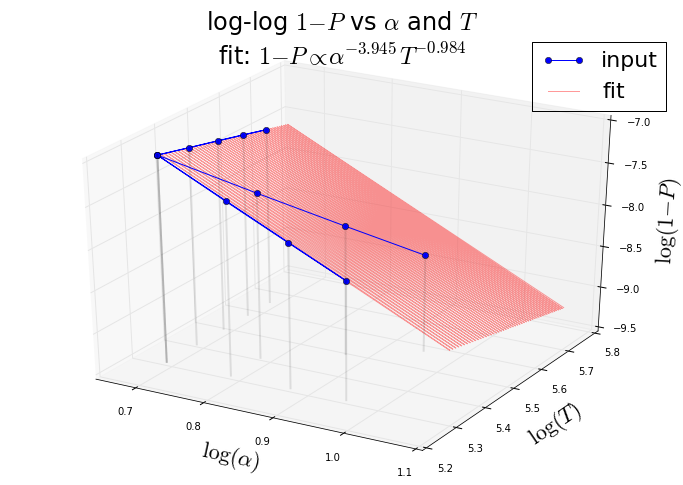
1−P∝α−3.9450T−0.984
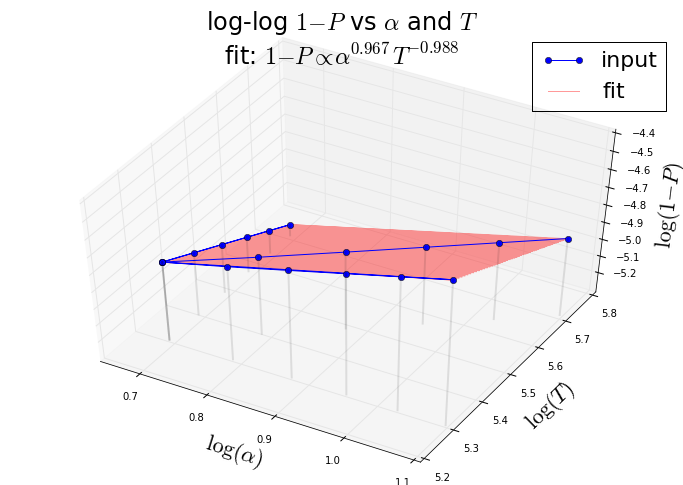
1−P∝α0.9670T−0.988
1−P∝α−1.8150v0.976
v∝1/T
1−P∝α−3.9450v0.984
v∝1/T
1−P∝α−0.0200v0.988
v∝α0/T


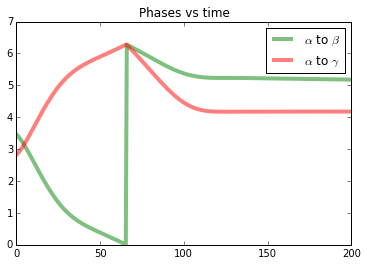
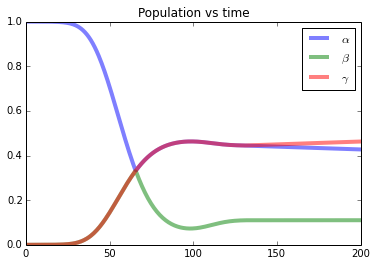
Each column in the table corresponds to a different gate. Just start by playing the animations.
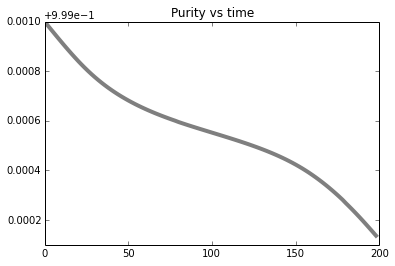
The dissipation coefficient is set to 1 in all simulations bellow. Therefore the time is dimensionless.
| Two Blobs | Three Blobs | ||||
|---|---|---|---|---|---|
| Phase Gate | Population Gate | Phase Gate | 2-Population Gate | 3-Population Gate | |
| Description | The right blob goes on a circle. | The two blobs collide. | The right blob goes on a circle. | Two of the three blobs collide. | The three blobs collide. |
| Initial State | |α0⟩+|−α0⟩ | |α0⟩ | |α0⟩+|3√−1α0⟩+|3√−12α0⟩ | |α0⟩+2|3√−1α0⟩ | |α0⟩ |
| Animation for α0=2 | |||||
| Scaling of the Purity wrt α0 and T |
1−P∝α−1.8150T−0.976 
|
1−P∝α−3.9450T−0.984 
|
1−P∝α0.9670T−0.988 
|
||
| Scaling of the Purity wrt α0 and v(the phase-space "speed" of the blobs) |
1−P∝α−1.8150v0.976 v∝1/T |
1−P∝α−3.9450v0.984 v∝1/T |
1−P∝α−0.0200v0.988 v∝α0/T |
||
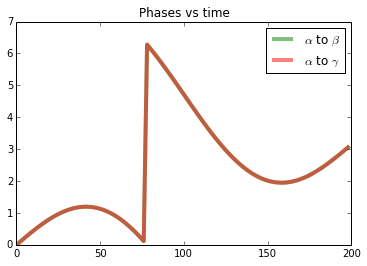
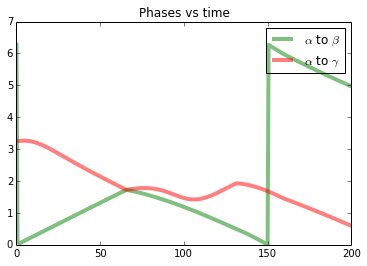
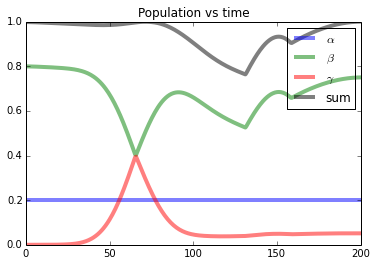
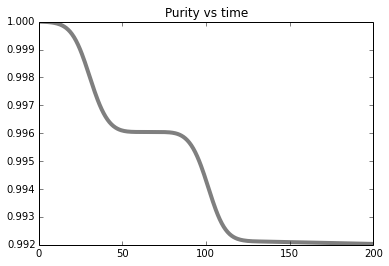
| The plots from the animation |



|



|



|
||
| Other remarks | Only the area matters for the induced phase. The loss in purity also seems to scale with the area, given that the results for a single circle of area A and for two circles each of area A/2 were the same (the total area was the same, the path taken was √2 bigger). See the next table. | For a fixed α0 the worst imperfections induced during the evolution are closer to the center. | Strange artefacts for the outer most blob, maybe due to cutoff dimension being too low. | For a fixed α0 the imperfections are induces mainly on the way into and out of the collision (not during the collision itself). | |
| Technical Details | Various, see the code. 15000 samples, N=80 cutoff for the (1-P) log log plot. 20000 samples, N=40 for the comparisons in the next table, 15000 samples, N=40 for the animation. | 60000 samples, N=40 cutoff | 200000 samples, N=55 cutoff (which is insufficient for α0>2.6) | 680000 samples, N=55 cutoff (possibly insufficient for these plots and animations) | 680000 samples, N=55 cutoff |
| Computer Code Files | phase gate, population gate, animation | visualization, simulation | visualization, simulation | visualization, simulation | |
| Two Blobs, Only the Right One Moving | Two Blobs Moving in Opposite Directions | |
|---|---|---|
| Plots and animations for various radiuses of the circles. | ||
| Description | The right blob goes on a circle. | Both blobs go on circles. The total area of the circles is the same as in the one-blob case. |
| Scaling of the Purity wrt α0 and T |
1−P∝α−1.8150T−0.976 
|
1−P∝α−1.7970T−0.974 
|
| The final relative phase between the blobs |
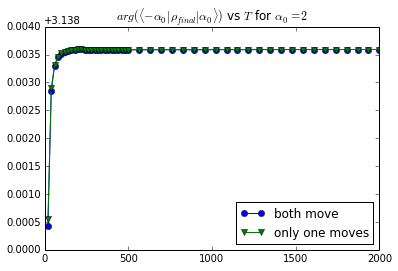
Total time T on the x axis |
|
| The final purity of the system |
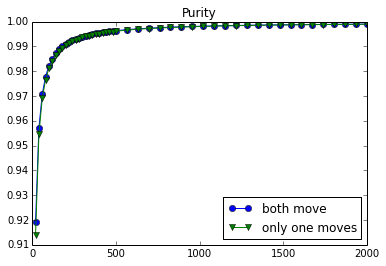
Total time T on the x axis |
|
| The contrast between the final purities for both approaches |
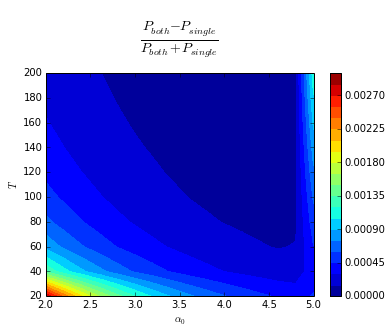
|
|